Factor base

In computational number theory, the factor base is a mathematical tool commonly used in algorithms involving extensive sieving of potential factors.

Usage

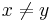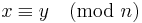The factor base is a relatively small set of prime numbers P. Say we want to factorize an integer n. We generate, in some way, a large number of integer pairs (x, y) for which $x \neq y$ and $\textstyle x \equiv y \pmod{n}$ , and x, y can be completely factorized over the chosen factor base—that is, they are p-smooth for the largest prime p in P.

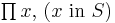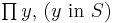We find a subset S of the integer pairs such that $\textstyle \prod_{} x \hbox{, } (x \hbox{ in } S)$ and $\textstyle \prod_{} y \hbox{, } (y \hbox{ in } S)$ are both perfect squares. Over our factor base this reduces to adding exponents of their prime factors, modulo 2, as we can distinguish squares from non-squares simply by checking the parity of the exponents.

We can represent each x and y as a vector of a matrix with 0 and 1 entries for the parity of each exponent. This essentially reformulates the problem into a system of linear equations, which can be solved using numerous methods such as Gaussian elimination; in practice advanced methods like the block Lanczos algorithm are used, that take advantage of certain properties of the system.

Once such a subset is found, we have essentially found a congruence of squares modulo n and can attempt to factorize n. This congruence may generate the trivial 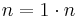$\textstyle n = 1 \cdot n$ ; in this case we try to find another suitable subset. If no such subset is found, we can search for more (x, y) pairs, or try again using a different factor base.

Algorithms

Factor bases are used in, for example, Dixon's factorization, the quadratic sieve, and the number field sieve. The difference between these algorithms is essentially the methods used to generate (x, y) candidates.